Usually GPUs do not support double precision. However, since it has become popular to utilize GPUs for computations of all sorts and the introduction of languages to support these efforts (like OpenCL, Cuda) it has become more and more important to support greater precision.
To improve performance of our mandelbrot project a little bit further, I will show how to use real, hardware accelerated double precision arithmetics.
Requirements
As we use OpenGL and GLSL for our shaders, we can use the OpenGL functions defined in the GL_ARB_gpu_shader_fp64 extension (see specification for details). This requires OpenGL 3.2 and GLSL 1.5 but you can try anyway…
Shader Code
The shader code is similar to the first part of this series with single floats only that I use double as data type. I also use double precision vector elements (dvec2) to make the code shorter. Please note that for some reason the length() function does not work with double precision vars (at least on my GPU, an ATI HD4870):
#version 150
uniform int iterations;
uniform int frame;
uniform float radius;
uniform dvec2 d_c;
uniform dvec2 d_s;
uniform double d_z;
float dmandel(void)
{
dvec2 c = d_c + dvec2(gl_TexCoord[0].xy)*d_z + d_s;
dvec2 z = c;
for(int n=0; n<iterations; n++)
{
z = dvec2(z.x*z.x - z.y*z.y, 2.0lf*z.x*z.y) + c;
if(length(vec2(z.x,z.y)) > radius)
{
return(float(n) + 1. - log(log(length(vec2(z.x,z.y))))/log(2.)); // http://linas.org/art-gallery/escape/escape.html
}
}
return 0.;
}
void main()
{
float n = dmandel();
gl_FragColor = vec4((-cos(0.025*n)+1.0)/2.0,
(-cos(0.08*n)+1.0)/2.0,
(-cos(0.12*n)+1.0)/2.0,
1.0);
}
Qt part
To access the shader variables from the main program we need functions suitable for double precision vars. OpenGL provides functions called glUniform1dv, glUniform2dv and so on. Unfortunately the Qt implementation does not (yet) support this function in their libraries. To overcome this situation we have to grab the handles to these functions directly from OpenGL. So let’s have a look at the glext.h. There you will find the definitions of these function. We add these to our project:
typedef void (APIENTRYP PFNGLUNIFORM1DVPROC) (GLint location, GLsizei count, const GLdouble *value);
PFNGLUNIFORM1DVPROC glUniform1dv;
typedef void (APIENTRYP PFNGLUNIFORM2DVPROC) (GLint location, GLsizei count, const GLdouble *value);
PFNGLUNIFORM2DVPROC glUniform2dv;
typedef GLint (APIENTRYP PFNGLGETUNIFORMLOCATIONPROC) (GLuint program, const GLchar *name);
PFNGLGETUNIFORMLOCATIONPROC glGetUniformLocation;
You may have noticed a third function called glGetUniformLocation. This function is required by the glUniformxdv functions to access the correct shader variable.
Now we grab the handles as follows:
glGetUniformLocation = (PFNGLGETUNIFORMLOCATIONPROC) GLFrame->context()->getProcAddress("glGetUniformLocation");
glUniform1dv = (PFNGLUNIFORM1DVPROC) GLFrame->context()->getProcAddress("glUniform1dv");
glUniform2dv = (PFNGLUNIFORM1DVPROC) GLFrame->context()->getProcAddress("glUniform2dv");
if(glGetUniformLocation && glUniform1dv && glUniform2dv) // did we get all handles?
{
qDebug() << "Yay! Hardware accelerated double precision enabled.";
RenderCaps |= 0x04; // yes, we can perform double precision rendering
}
else qDebug() << "Too bad, your GPU does not support hardware accelerated double precision.";
After that is done, we can use these function to feed our double precision mandelbrot shader shader as follows:
double tmp, dvec2[2];
// snip
case 2: // double precision (FP64) shader values
dvec2[0] = xpos;
dvec2[1] = ypos;
glUniform2dv(glGetUniformLocation(ShaderProgram->programId(), "d_c"), 2, dvec2);
dvec2[0] = -((double)w)/2.0/zoom;
dvec2[1] = -((double)h)/2.0/zoom;
glUniform2dv(glGetUniformLocation(ShaderProgram->programId(), "d_s"), 2, dvec2);
tmp = 1./zoom;
glUniform1dv(glGetUniformLocation(ShaderProgram->programId(), "d_z"), 1, &tmp);
break;
Benchmark
To benchmark the emulated and hardware accellerated double precision I used the following settings:
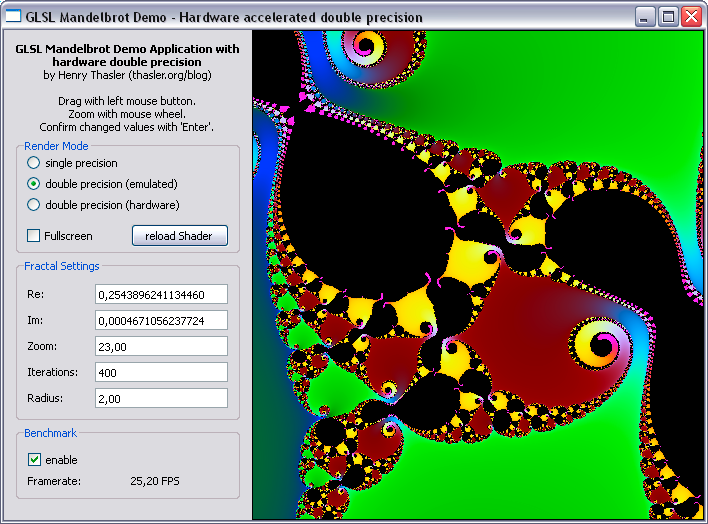
| Method | FPS |
|---|---|
| single precision | 120 |
| emulated double precision | 25 |
| hardware double precision | 90 |
As expected the hardware supported version is almost 4 times faster that the emulated. Hopefully more GPUs support double precision in the future.
Sourcecode
Conclusion
Hardware acellerated double precision rendering works fine on supported GPUs. In our mandelbrot demo it is much faster than emulated an also gives a detail boost of about four zoom steps (47 vs. 43).
But I guess this is not the end of the line. I’m sure I can improve accuracy even more. Stay tuned.