In my last post I introduced a simple mandelbrot fractal shader with GLSL. —Unfortunately— Intentionally, the shader code uses single precision floating point variables which ensures great performance but limits the zoom factor to about 17 before the lack of accuracy of the floating point variables takes over and all you get is a block-ish image of some sort at greater zoom levels:
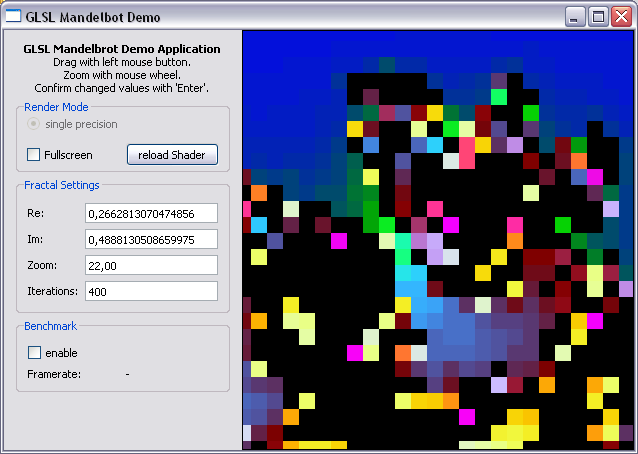
Since I am very interested to discover the beauty of our mandelbrot set in close detail I will improve the existing shader with emulated double precision variables (aka: double-single) and see how far I can push it.
Basics about precision emulation
Since I didn’t find any GLSL code samples using emulated precision I decided to use the DSFUN90 library by David H. Bailey which is written in Fortran. Fontran is no good for GPUs so I had to convert the parts I needed to GLSL.
Single precision floats can hold up to 8 digits and an exponent. Say, when you want to store the numer 0.4888129819481270 in a single float variable you will get 4.8881298e-1 (8 digits and an exponent). The remainder (the green part) is lost. On the other hand you can store the number 0.0000000019481270 in a single float without having any trouble (1.9481270e-9). Check out this page to convert any number to their single or double precision counterparts and see what happens.
You may have figured out by now, that you can store the number 0.4888129819481270 as the sum of 4.8881298e-1 and 1.9481270e-9 and that it is possible to store each of these two parts in a single floating point variable. So we just split the double precision value in two single precision variables as shown above and we are fine. Well, we’re almost fine, since the functions to do the basic math stuff like addition or multiplication get a bit more complicated but that’s the point where Mr. Bailey’s library comes in and helps us out with his emulated double precision arithmetic.
Main Application
Preparing the double precision variables before transferring the to our shader works as described above:
- take a double (0.4888129819481270) and convert it to single float (4.8881298e-1). Store it.
- convert the single float back to double (0.4888129800000000) and subtract it from our original value.
- Store the result (0.0000000019481270) in the second float (1.9481270e-9).
vec2[0] = (float)xpos;
vec2[1] = xpos - (double)vec2[0];
ShaderProgram->setUniformValue("ds_cx0", vec2[0]);
ShaderProgram->setUniformValue("ds_cx1", vec2[1]);
The blue and green parts can be seen as High- and Low-Part of our emulated double value.
Emulated arithmetics
The emulated double precision values (double-single) can be stored as vec2 in GLSL. This makes the code short and readability is improved (vec2(ds_hi, ds_lo)).
To evaluate our mandelbrot formula (z = vec2(z.x*z.x - z.y*z.y, 2.0*z.x*z.y) + c) and do the other stuff to create a cool looking image, we need the following arithmetics:
- Convert to/from emulated double precision (double-single)
- Addition, subtraction
- Multiplication
- Comparison
Conversion to double-single is easy since you just copy the value to the High part of the double-single (DS) variable.
vec2 ds_set(float a)
{
vec2 z;
z.x = a;
z.y = 0.0;
return z;
}
vec2 ds_two = ds_set(2.0);
To create a single float from our DS variable we just use the High-part and leave the (much smaller) Low-part out. float s_two = ds_two.x; Addition is a bit more complex since you have to take care of some carry over from low to high part.
vec2 ds_add (vec2 dsa, vec2 dsb)
{
vec2 dsc;
float t1, t2, e;
t1 = dsa.x + dsb.x;
e = t1 - dsa.x;
t2 = ((dsb.x - e) + (dsa.x - (t1 - e))) + dsa.y + dsb.y;
dsc.x = t1 + t2;
dsc.y = t2 - (dsc.x - t1);
return dsc;
}
Multiplication is even more weird…
vec2 ds_mul (vec2 dsa, vec2 dsb)
{
vec2 dsc;
float c11, c21, c2, e, t1, t2;
float a1, a2, b1, b2, cona, conb, split = 8193.;
cona = dsa.x * split;
conb = dsb.x * split;
a1 = cona - (cona - dsa.x);
b1 = conb - (conb - dsb.x);
a2 = dsa.x - a1;
b2 = dsb.x - b1;
c11 = dsa.x * dsb.x;
c21 = a2 * b2 + (a2 * b1 + (a1 * b2 + (a1 * b1 - c11)));
c2 = dsa.x * dsb.y + dsa.y * dsb.x;
t1 = c11 + c2;
e = t1 - c11;
t2 = dsa.y * dsb.y + ((c2 - e) + (c11 - (t1 - e))) + c21;
dsc.x = t1 + t2;
dsc.y = t2 - (dsc.x - t1);
return dsc;
}
Smooth coloring
I have also improved the coloring method to smooth, continuous coloring as described in this post by Linas Vepstas or on wikipedia.
if(length(z) > radius)
{
return(float(n) + 1. - log(log(length(z)))/log(2.));
}
Don’t be scared of all that logarithm stuff. Most modern GPU can handle these very well.
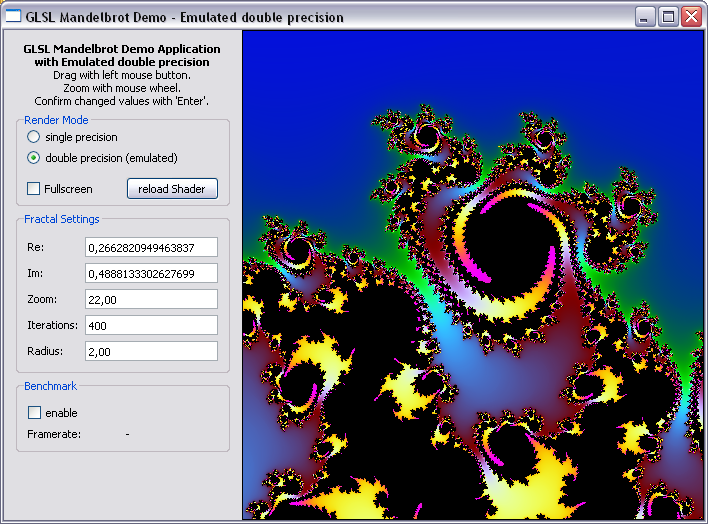
Result
Starting with our block example above the emulation shows excellent details for zoom levels up to 42 before the precision of our emulated doubles is spent:
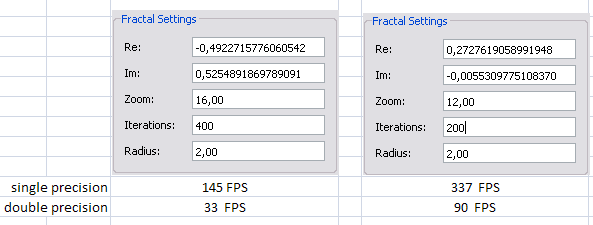
Performance
I get the following framerates in benchmark mode on my desktop ATI HD4870. They show that the emulation is round about 4 times slower than single precision mode. But still qualifies for realtime rendering.
Conclusion
Compared to single precision with a maximum resolution of units in the complex plane per pixel the emulated doubles perform well up to
units per pixel.
Emulated double precision is a cool thing to do and works quite well on modern GPUs. Let’s see if there can be done something to improve accuracy further…
Qt Sourcecode
Sourcecode: GLSL_EmuMandel.zip