Heavy computing with GLSL

In my previous GLSL post I have shown how to draw a white quad. Since this is not the greatest visual experience, I will show something more interesting you can do with shaders in this post.

I have chosen the famous mandelbrot fractal. It’s nice and colorful. Quite a fine eyecatcher.

Sourcecode: GLSL_SimpleMandel.zip

The code was tested on WinXP/ATI-GPU and Win7/NVidia-GPU

The final result looks like this:

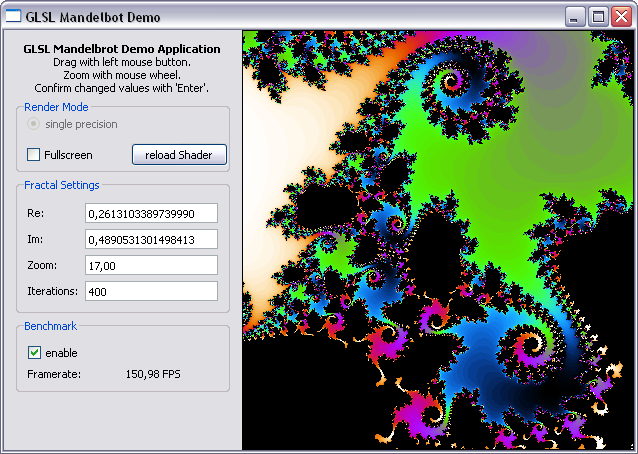
First Steps

Let’s see what we need:

user interface (short help, fancy settings textboxes)
render area (the colorful thingy)
fractal navigation (like zoom, drag, position info)
mandelbrot algorithm/background information
GLSL shader

User Interface

The user interface can be set up with the Qt designer. There are some pitfalls when designing graphical UIs with Qt, namely:

Make sure you set the “Horizontal Policy” of the QLineEdit-Objects to “Minimum”. Otherwise they will break your layout.
You need a QGridLayout to place a Widget. A QFrame is not sufficient.

Render Area

Since we want to set the color for each pixel according to some obscure fractal formula (see below) we don’t need fancy stuff like 3D projection, so our OpenGL init function is really short:

void QGLRenderThread::GLInit(void)
{
    glClearColor(0.25f, 0.25f, 0.4f, 0.0f);     // Background => dark blue
    glDisable(GL_DEPTH_TEST);
    glEnable(GL_TEXTURE_2D);

    const GLubyte* pGPU = glGetString(GL_RENDERER);
    const GLubyte* pVersion = glGetString(GL_VERSION);
    const GLubyte* pShaderVersion = glGetString(GL_SHADING_LANGUAGE_VERSION);

    qDebug() << "GPU: " << QString((char*)pGPU).trimmed();
    qDebug() << "OpenGL: " << QString((char*)pVersion).trimmed();
    qDebug() << "GLSL: " << QString((char*)pShaderVersion);
}

Set the background color, disable depth testing, enable textures and show some debug information about your current hardware configuration, OpenGL and GLSL version.

When resizing the window we use glOrtho instead of glPerspective to make our OpenGL coorinate space the same size as our window:

void QGLRenderThread::GLResize(int width, int height)
{
    glViewport(0, 0, width, height);
    glMatrixMode(GL_PROJECTION);

    glLoadIdentity();

    glOrtho (0, w, 0, h, 0, 1);

    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
}

With this setting the lower left corner represents the origin of the OpenGL coordinate system.

To navigate in our mandelbrot set we use a left-mouse-button drag function.

The zoom function is combined with a point-and-zoom feature. This gives you the possibility to zoom into the area around the mouse cursor (like on google maps). Looks complicated and it is, since it took me a while to figure it out…

void QGLFrame::wheelEvent(QWheelEvent * event)
{
  RenderThread.Zoom( (event->delta()>0), event->pos(), 2.0);
  updateLabels(event->pos());
  RenderThread.Redraw();
}

In the Thread:

void QGLRenderThread::Zoom(bool dir, const QPoint &pos, double zfact)
{
    double c;

    c = xpos+(pos.x()-w/2)/zoom;
    xpos = (xpos+((dir)?1.0:-1.0)*(c-xpos)*((dir)?(1.0-1.0/zfact):(zfact-1.0)));

    c = ypos-(pos.y()-h/2)/zoom;
    ypos = (ypos+((dir)?1.0:-1.0)*(c-ypos)*((dir)?(1.0-1.0/zfact):(zfact-1.0)));

    zoom*=(dir)?zfact:(1.0/zfact);
}

Information about the current position is displayed in editfields on the left. We employ a signal/slot mechanism for this purpose since the editfields in Qt can handle this pretty easily:

void QGLFrame::updateLabels(const QPoint &pos)
{
  double x,y;
    RenderThread.getMousePosition(x,y, pos);
    emit showRePosition(QString("%L1").arg(x,0,'f',16));
    emit showImPosition(QString("%L1").arg(y,0,'f',16));
    RenderThread.getZoom(y);
    emit showZoomValue(QString("%L1").arg(log2(y/128.),0,'f',2));
    emit showIterationsValue(QString("%1").arg(RenderThread.getIterations()));
}

GLSL Mandelbrot Shader

To render a mandelbrot fractal you have to evaluate the following equation for every pixel: (image: https://latex.codecogs.com/png.download?z_{n+1}=z_{n}^2+c) Where c is the corresponding point in the complex plane for this pixel. The color of this pixel is defined by the number of iterations after |z|>2.

This is the vertex shader:

#version 120

void main(void)
{
  gl_TexCoord[0] = gl_MultiTexCoord0;
  gl_Position    = ftransform();
}

The vertex shader only sets the texture coordinates of our window-sized textured rectangle where the lower left window corner represents the texture coordinates (0/0) and the upper right corner the texture coordinates (windowwidth/windowheight). This area represents the first quadrand of the cartesian coordinate system.

The mandelbrot calculation is performed in the following fragment shader program:

#version 120

uniform int iterations;
uniform float frame;
uniform float radius;

uniform float f_cx, f_cy;
uniform float f_sx, f_sy;
uniform float f_z;

int fmandel(void)
{
  vec2 c = vec2(f_cx, f_cy) + gl_TexCoord[0].xy*f_z + vec2(f_sx,f_sy);
  vec2 z=c;

  for(int n=0; n<iterations; n++)
        {
        z = vec2(z.x*z.x - z.y*z.y, 2.0*z.x*z.y) + c;
        if((z.x*z.x + z.y*z.y) > radius) return n;
        }
  return 0;
}

void main()
{
  int n = fmandel(); 

  gl_FragColor = vec4((-cos(0.025*float(n))+1.0)/2.0,
                      (-cos(0.08*float(n))+1.0)/2.0,
                      (-cos(0.12*float(n))+1.0)/2.0,
                      1.0);
}

The function fmandel is used to compute the iterations needed for the aforementioned equation. The constant c representing the current pixel in the complex plane is derived by the texture coordinates, the center and the zoom factor (given by the uniform values).

We can use the vec2 data-type to simplify addition of complex numbers, but have to keep in mind that multiplicating complex numbers is something different.

The color of a pixel is derived from the number of iteration and some cosine function that gives black for n=0 and otherwise a colorful gradient.

Render Thread and Benchmark Mode

The render thead is designed to run only when needed and is put to sleep when no updates of the fractal set are required. This can be done with the QWaitCondition and QMutex objects. It prevents the GPU from unnessessary load and leaves the CPU for other tasks/applications.

As the user zooms/drags or changes the window size the thread wakes up and initiates an update via the fractal shader.

To test ther performance of your hardware setup or if you want to play around with other shaders and compare the performances, you can enable the benchmark checkbox to evaluate the maximum framerate when the rendering is performed continuously.

To measure the exact framerateI use the QueryPerformanceCounter. Unfortunately this is only available under win and has some problems. See this blog for reasons not to use it. If anyone has an idea what to use instead please let me know.

Please also note that the framerate largely depends on the number of iterations, the center position you are looking at and of course the window size since the calculation is performed for every pixel in the window.

Summary

We have shown a simple mandelbrot implementation with Qt and OpenGL that shows great performance results and allows real time updates of the mandelbrot set even on mobile GPUs.

Unfortunately the zoom factor is limited by the floating point precision used to perform the calculation. Zoom factors of 18 or more lead to larger pixels not showing more details:

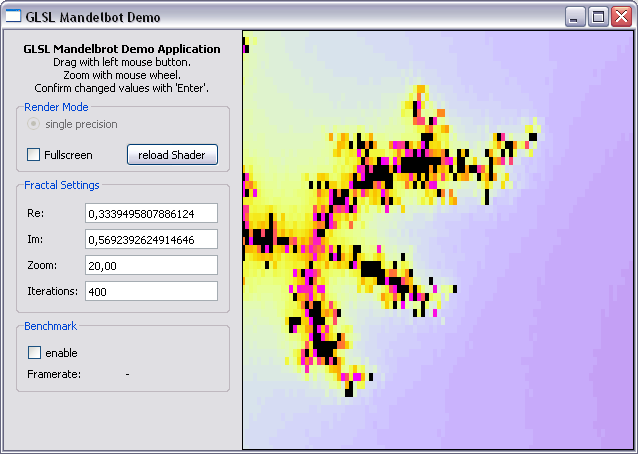
A method to improve accuracy is to emulate double precision on the GPU or even use double precision variables as it is possible on some graphics card.

This will be subject of the next part in our “heavy computing” series.

Heavy computing with GLSL - Part 1

Basics